Overview
The primary purpose of the ramp motion simulation is to provide students a realistic environment where they can explore and better understand the concepts in Newtonian mechanics using fundamental mechanics methods. In the mechanics simulation, experiments are performed in a framework consistent with the other virtual simulations; that is, students are put into a virtual environment where they are free to choose their objects and equipment, build a conceptual experiment of their own design, and then experience the resulting consequences. The focus in the mechanics simulation is to allow students the flexibility to perform many fundamental experiments to teach the basic concepts of Newton’s laws that are easier to model in a simulated situation rather than a real laboratory. The ability to control the frictions, forces, and physical parameters of motion allows students the ability to easily use equipment that can be found in most instructional laboratories and some equipment that would be less readily available. Students are able to measure speeds and distances, describe the motion of objects using graphs, interpret data and gain a foundation for concepts in physics. These results can then be used to validate Newton’s laws; demonstrate the interplay between force and motion; and calculate conservation of momentum under variable initial conditions and parameters.
Simulation Principles and Features
Ramp Motion. Planar motion is the focus of motion experiments on an inclined plane. Motion without slipping and with slipping is presented so students can investigate the effects of surface friction on the motion of an object. Rotational velocity and angular acceleration are displayed to teach how the angle and material of the ramp affects the rotational and translational motion. Various materials are simulated so students can learn about coefficients of friction. All mechanics experiments allow students to record data from the equations of motion for later graphical and numerical analysis, which in the case of ramp motion is very useful because of the difficulty of obtaining real life data without complex equipment. Ramp experiments can be set up with either uniform downward gravity or a radial gravity source within the ramp. Traditional ramp experiments can be set up with uniform downward gravity and a ball set on the ramp. By choosing the materials of the ball and ramp, the kinetic and static coefficients of friction are set and air resistance and forces can then be applied to enhance the experiment. The radial gravity source can be used to teach oscillating motion with or without damping. The radial gravity is set inside of the ramp and the chosen object can be observed oscillating up and down the ramp over the point sink.
Simulation Assumptions and Equations
Ramp Motion. Newtonian force equations were used as the equations of motion for simulating the ramp motion experiments. All force equations were solved using a Runge Kutta Fehlberg Forth-Fifth (RKF45) numerical method to solve the differential equations. The one second derivative equation was manipulated into two first order equations and then integrated through RKF45 to find the position and the velocity equations of motion of the objects. The friction force is a linear force dependent only on the coefficient of kinetic friction and the force of gravity. The friction can be strong enough that the initial conditions of the ball do not permit it to overcome the static friction barrier, but once the object starts moving, the frictional force is constant and is not dependent on the velocity.
| Objects | The ball rolling down the inclined plane can be either a solid or hollow sphere. The material density affects the moment of inertia of the ball, which is manifest under the rolling conditions. The ball is assumed to be perfectly circular with no deformities; therefore it touches the ground at exactly one point. The balls can either slide or roll without slipping when on the ramp. The rolling has been modeled as idealized rolling without slipping, which means that there is no friction once the rolling condition is reached. The sled slides on the ramp with a constant frictional force resisting the direction of motion. To see damped oscillating motion on a ramp with radial gravity, the sled is the best option, since it does not encounter rolling conditions. |
| Ramp | The ramp surface can be made of different materials to set the friction coefficient. The surface has no imperfections, and is uniformly consistent in the chosen texture. For non-friction experiments the ramp is considered perfectly smooth. It can be set to any angle between 0 to 90 degrees. |
| Gravity | Uniform gravity down and radial gravity are the only gravities that can be applied to the ramp. Radial gravity, when applied to the ramp, is located directly below the center of the ramp perpendicular to the surface at a distance the user chooses. The default distance is 1 m. |
| Rolling | The friction icon is what is used to apply friction between a ball and the table. The simulation calculates the point at which perfect rolling without sliding occurs and applies sliding friction to the ball until that point. When the rotational velocity of the ball reaches the critical barrier to roll without slipping, then the ball just rolls with no frictional forces being applied. The assumption is taken that the perfectly round ball only comes in contact with the ground at exactly one spot and when perfectly rolling, the velocity of the ball at that point is zero, so no forces act upon it. For this reason, once a ball reaches perfect rolling conditions, it will roll without resistance. |
| Sliding | Here we assume the sled will slide uniformly, and the surface area will determine the amount of friction being generated. |
The assumptions and limitations of forces and air resistance are described below as they are common to multiple experiments.
Forces. The forces applied in the lab can be one of two types, a rocket force or a plunger force. The rocket force is a continual force of a chosen magnitude which can either be applied for a set time period or indefinitely. The impulse force (plunger) hits the object with a chosen magnitude for a short period (default 0.05 seconds) of time thus giving the object an almost instantaneous initial velocity. The assumptions are those of a perfect rocket force with no flaws in ignition and an exact central hit from the plunger to prevent spin.
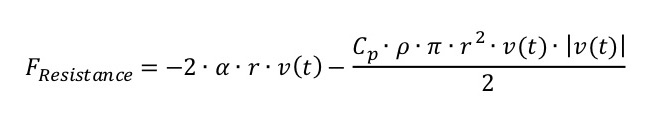
Frictions. A friction is considered something that opposes an object’s motion. In these simulations there are three types of frictions available. Some depend on the speed of the moving object and others depend on the surface area of the object. The rolling and sliding friction were described previously under ramp motion. For air friction, we have combined linear and quadratic air resistance terms to create a general air resistance. Linear air resistance is modeled proportional to the velocity, radius, and a constant generally agreed to be α = 0.000155. The quadratic air resistance term is proportional to the cross-sectional area of the object, the air density at the chosen altitude, the square of the velocity and a constant describing the irregularity of the surface Cp = 0.5 for the ball and Cp = 1.0 for the sled. A larger value for this constant could be chosen to model a much more irregular object, up to a value of 2. The equation to the right is what is used to apply the air resistance.
